ドキュメント

Computer Science

アルゴリズム

探索アルゴリズム

探索アルゴリズム

探索(たんさく) アルゴリズムの学習(がくしゅう) ノート。

配列探索アルゴリズム

これらのアルゴリズムは主(おも) にソート済(ず) みまたは未(み) ソートの配列(はいれつ) での検索(けんさく) に使用(しよう) される
どのアルゴリズムを選択(せんたく) するかは、データがソートされているか、データセットのサイズ、検索頻度(けんさくひんど) に依存(いぞん) する

アルゴリズム	利点(りてん)	欠点(けってん)	使用場面(しようばめん)
線形探索(せんけいたんさく)	実装(じっそう) が簡単(かんたん) 、未(み) ソートデータに対応(たいおう)	大規模(だいきぼ) データセットでは非効率(ひこうりつ)	小規模(しょうきぼ) データセット
二分探索(にぶんたんさく)	高効率(こうこうりつ)	データが事前(じぜん) にソートされている必要(ひつよう) あり	大規模(だいきぼ) ソート済(ず) みデータ
補間探索(ほかんたんさく)	均一分布(きんいつぶんぷ) データでは非常(ひじょう) に高速(こうそく)	非均一分布(ひきんいつぶんぷ) データでは非効率(ひこうりつ)	大規模(だいきぼ) 均一分布(きんいつぶんぷ) 数値配列(すうちはいれつ)

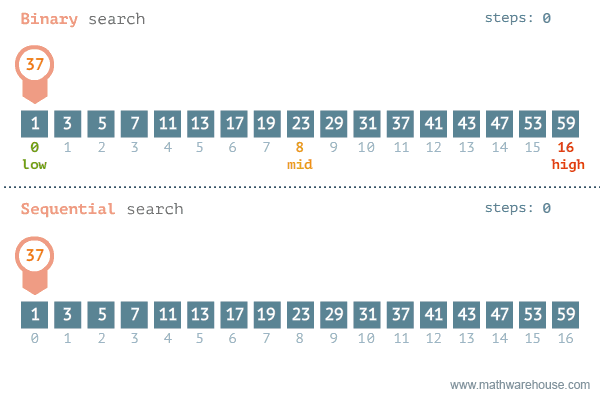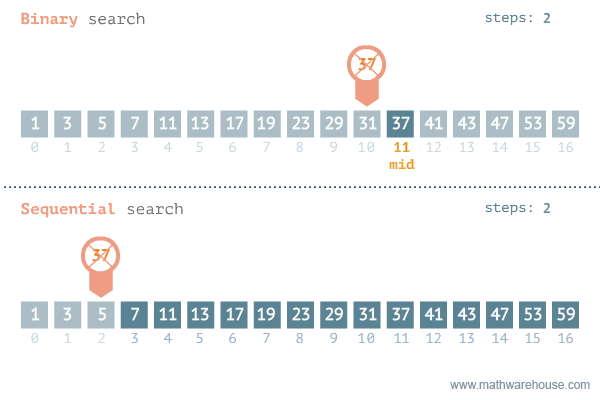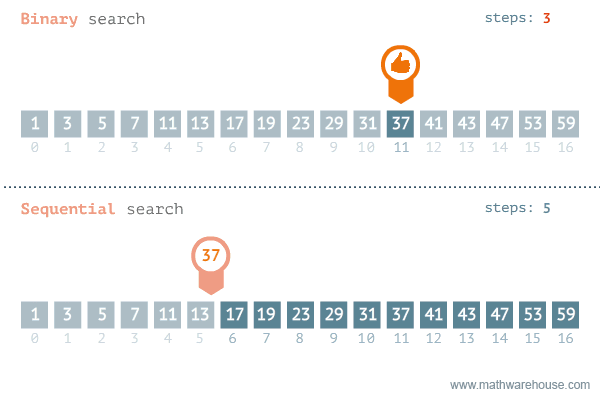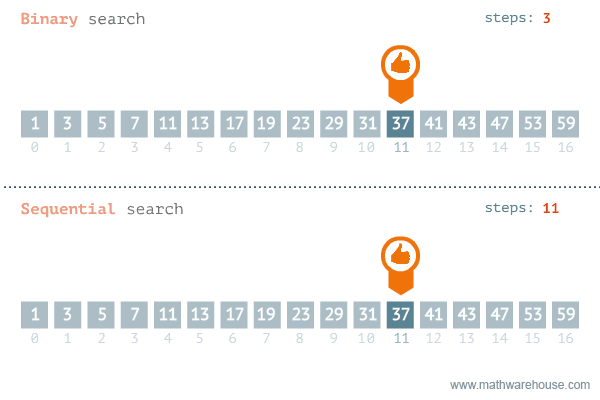
Binary Search

二分探索(にぶんたんさく) - ソート済(ず) み配列(はいれつ) で効率的(こうりつてき) に目標値(もくひょうち) を検索(けんさく)

Time Complexity
- Best: $O(1)$
- Average: $O(\log n)$
- Worst: $O(\log n)$
Space Complexity:
- 反復(はんぷく) : $O(1)$
- 再帰(さいき) : $O(\log n)$

Interpolation Search

補間探索(ほかんたんさく) - 均一分布(きんいつぶんぷ) データに最適化(さいてきか) された探索(たんさく) アルゴリズム

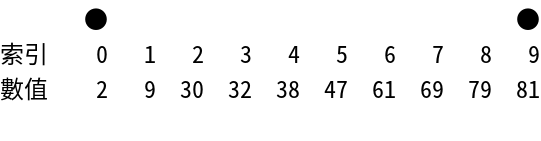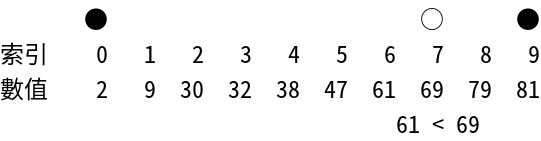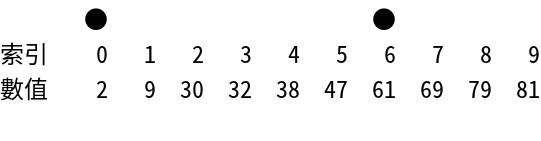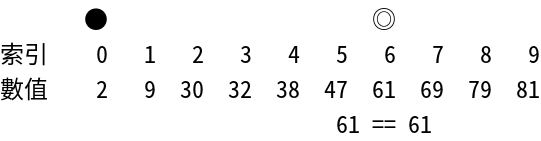
Time Complexity
- Best: $O(1)$
- Average (均一分布(きんいつぶんぷ) データ): $O(\log(\log n))$
- Worst: $O(n)$
Space Complexity: $O(1)$

グラフ探索アルゴリズム

これらのアルゴリズムはグラフ構造(ぐらふこうぞう) （ソーシャルネットワーク、地図(ちず) など）での経路(けいろ) や特定(とくてい) ノードの検索(けんさく) に使用(しよう) される

アルゴリズム	利点(りてん)	欠点(けってん)	使用場面(しようばめん)
深(ふか) さ優先探索(ゆうせんたんさく) (DFS)	メモリ効率(こうりつ) が良(よ) い	深(ふか) い分岐(ぶんき) に陥(おちい) る可能性(かのうせい)	迷路解決(めいろかいけつ) 、トポロジカルソート
幅優先探索(はばゆうせんたんさく) (BFS)	最短経路(さいたんけいろ) を発見(はっけん)	メモリ消費(しょうひ) が大(おお) きい	最短経路問題(さいたんけいろもんだい)
Dijkstra法(ほう)	単一始点最短経路(たんいつしてんさいたんけいろ) を発見(はっけん)	負(ふ) の重(おも) みには非対応(ひたいおう)	ナビゲーション、ネットワークルーティング
A*探索(たんさく)	最良優先探索(さいりょうゆうせんたんさく) とヒューリスティックの組(く) み合(あ) わせ	ヒューリスティック関数(かんすう) の選択(せんたく) が効率(こうりつ) に影響(えいきょう)	経路計画(けいろけいかく) 、ゲームAI

文字列探索アルゴリズム

主(おも) にテキスト処理(しょり) 、パターンマッチングに使用(しよう) される

アルゴリズム	利点(りてん)	欠点(けってん)
KMP法(ほう)	効率的(こうりつてき) な文字列(もじれつ) マッチング	実装(じっそう) が複雑(ふくざつ)
Rabin-Karp法(ほう)	複数(ふくすう) パターンを同時(どうじ) に検索可能(けんさくかのう)	ハッシュ関数(かんすう) の選択(せんたく) が効率(こうりつ) に影響(えいきょう)
Boyer-Moore法(ほう)	実用上(じつようじょう) 他(ほか) の文字列(もじれつ) アルゴリズムより優秀(ゆうしゅう)	前処理(まえしょり) が複雑(ふくざつ)

確率的探索アルゴリズム

これらのアルゴリズムは通常(つうじょう) 、複雑(ふくざつ) な最適化問題(さいてきかもんだい) や大規模(だいきぼ) な探索空間(たんさくくうかん) に使用(しよう) される

アルゴリズム	利点(りてん)	欠点(けってん)
モンテカルロ木探索(きたんさく) (MCTS)	大(おお) きな状態空間(じょうたいくうかん) に適用可能(てきようかのう)	良(よ) い結果(けっか) を得(え) るには多(おお) くのシミュレーションが必要(ひつよう)
焼(や) きなまし法(ほう)	局所最適解(きょくしょさいてきかい) から脱出可能(だっしゅつかのう)	大域最適解(たいいきさいてきかい) の発見(はっけん) は保証(ほしょう) されない
遺伝的(いでんてき) アルゴリズム	複雑(ふくざつ) な最適化問題(さいてきかもんだい) を処理可能(しょりかのう)	パラメータ調整(ちょうせい) が複雑(ふくざつ)

特殊探索アルゴリズム

ハッシュ探索(たんさく) とブルームフィルタは大規模(だいきぼ) データセットの高速検索(こうそくけんさく) に使用(しよう) される

アルゴリズム	利点(りてん)	欠点(けってん)
ハッシュ探索(たんさく)	ハッシュテーブルで定数時間(ていすうじかん) に近(ちか) い検索(けんさく)	追加(ついか) ストレージが必要(ひつよう) 、ハッシュ衝突(しょうとつ) の可能性(かのうせい)
ブルームフィルタ	空間効率(くうかんこうりつ) が高(たか) い、検索(けんさく) が高速(こうそく)	偽陽性(ぎようせい) の可能性(かのうせい) あり、削除非対応(さくじょひたいおう)